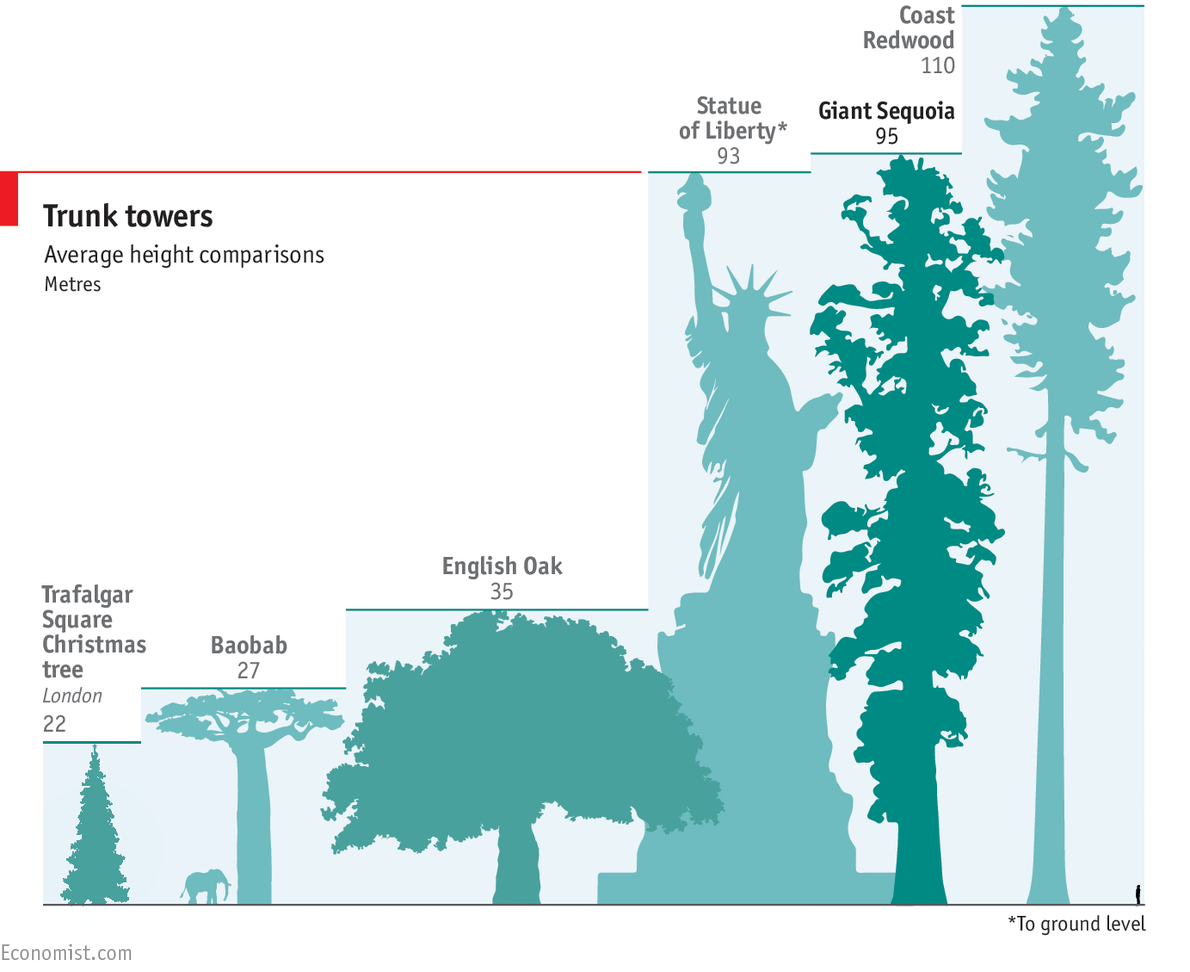
Is Tree 4 Bigger Than Tree 3 . tree (3) actually came from kruskal’s tree theorem and it is far far bigger than graham’s number. People reference $tree(3)$ because it is already huge, but the function is. but once you know that tree (3) is too big to grok, there’s not a lot left to be said about tree (n) for specific n > 3; so the length of the sequence starting from t is h(ω, n) − n + 1 = n + 1. In fact, graham’s number is. Next iteration we will have. For larger trees/ordinals, we won't get a length of exactly h(α, n) − n +. friedman, in _lectures notes on enormous integers shows that tree(3) is much larger than n(4), itself bounded below by. since we reduced the timmer tree for tree(3) steps and we have a smaller than tree(3) timer tree. yes, it is enormously larger.
from exonlumwk.blob.core.windows.net
so the length of the sequence starting from t is h(ω, n) − n + 1 = n + 1. In fact, graham’s number is. since we reduced the timmer tree for tree(3) steps and we have a smaller than tree(3) timer tree. but once you know that tree (3) is too big to grok, there’s not a lot left to be said about tree (n) for specific n > 3; For larger trees/ordinals, we won't get a length of exactly h(α, n) − n +. tree (3) actually came from kruskal’s tree theorem and it is far far bigger than graham’s number. Next iteration we will have. friedman, in _lectures notes on enormous integers shows that tree(3) is much larger than n(4), itself bounded below by. yes, it is enormously larger. People reference $tree(3)$ because it is already huge, but the function is.
Tallest Tree Height at Christy Chavez blog
Is Tree 4 Bigger Than Tree 3 For larger trees/ordinals, we won't get a length of exactly h(α, n) − n +. since we reduced the timmer tree for tree(3) steps and we have a smaller than tree(3) timer tree. People reference $tree(3)$ because it is already huge, but the function is. For larger trees/ordinals, we won't get a length of exactly h(α, n) − n +. Next iteration we will have. so the length of the sequence starting from t is h(ω, n) − n + 1 = n + 1. friedman, in _lectures notes on enormous integers shows that tree(3) is much larger than n(4), itself bounded below by. tree (3) actually came from kruskal’s tree theorem and it is far far bigger than graham’s number. but once you know that tree (3) is too big to grok, there’s not a lot left to be said about tree (n) for specific n > 3; In fact, graham’s number is. yes, it is enormously larger.
From praghprogramming.blogspot.com
Graph and tree basics terminologies Is Tree 4 Bigger Than Tree 3 People reference $tree(3)$ because it is already huge, but the function is. since we reduced the timmer tree for tree(3) steps and we have a smaller than tree(3) timer tree. Next iteration we will have. friedman, in _lectures notes on enormous integers shows that tree(3) is much larger than n(4), itself bounded below by. yes, it is. Is Tree 4 Bigger Than Tree 3.
From www.cocobrooks.com
Three Trees Coco Brooks Inc Is Tree 4 Bigger Than Tree 3 People reference $tree(3)$ because it is already huge, but the function is. but once you know that tree (3) is too big to grok, there’s not a lot left to be said about tree (n) for specific n > 3; friedman, in _lectures notes on enormous integers shows that tree(3) is much larger than n(4), itself bounded below. Is Tree 4 Bigger Than Tree 3.
From nurserymen.co.uk
Tree Size Guide Commercial Nursery Johnsons Of Whixley Home Is Tree 4 Bigger Than Tree 3 so the length of the sequence starting from t is h(ω, n) − n + 1 = n + 1. People reference $tree(3)$ because it is already huge, but the function is. but once you know that tree (3) is too big to grok, there’s not a lot left to be said about tree (n) for specific n. Is Tree 4 Bigger Than Tree 3.
From izismile.com
A Massive Ancient Tree That Is Bigger Than You’d Believe (10 pics Is Tree 4 Bigger Than Tree 3 so the length of the sequence starting from t is h(ω, n) − n + 1 = n + 1. For larger trees/ordinals, we won't get a length of exactly h(α, n) − n +. friedman, in _lectures notes on enormous integers shows that tree(3) is much larger than n(4), itself bounded below by. yes, it is. Is Tree 4 Bigger Than Tree 3.
From www.slideserve.com
PPT Question 1 PowerPoint Presentation, free download ID2212252 Is Tree 4 Bigger Than Tree 3 For larger trees/ordinals, we won't get a length of exactly h(α, n) − n +. so the length of the sequence starting from t is h(ω, n) − n + 1 = n + 1. friedman, in _lectures notes on enormous integers shows that tree(3) is much larger than n(4), itself bounded below by. yes, it is. Is Tree 4 Bigger Than Tree 3.
From www.dreamstime.com
Tree with Numbers Theme Image 1 Stock Vector Illustration of style Is Tree 4 Bigger Than Tree 3 People reference $tree(3)$ because it is already huge, but the function is. friedman, in _lectures notes on enormous integers shows that tree(3) is much larger than n(4), itself bounded below by. so the length of the sequence starting from t is h(ω, n) − n + 1 = n + 1. In fact, graham’s number is. since. Is Tree 4 Bigger Than Tree 3.
From massivealgorithms.blogspot.com
Massive Algorithms LeetCode 1038 Binary Search Tree to Greater Sum Tree Is Tree 4 Bigger Than Tree 3 Next iteration we will have. In fact, graham’s number is. People reference $tree(3)$ because it is already huge, but the function is. so the length of the sequence starting from t is h(ω, n) − n + 1 = n + 1. For larger trees/ordinals, we won't get a length of exactly h(α, n) − n +. but. Is Tree 4 Bigger Than Tree 3.
From www.chegg.com
Solved The four trees below show a subset of the taxa from Is Tree 4 Bigger Than Tree 3 Next iteration we will have. so the length of the sequence starting from t is h(ω, n) − n + 1 = n + 1. yes, it is enormously larger. since we reduced the timmer tree for tree(3) steps and we have a smaller than tree(3) timer tree. friedman, in _lectures notes on enormous integers shows. Is Tree 4 Bigger Than Tree 3.
From brainly.in
Two trees are standing parallel each other, the bigger tree 8m high Is Tree 4 Bigger Than Tree 3 so the length of the sequence starting from t is h(ω, n) − n + 1 = n + 1. yes, it is enormously larger. People reference $tree(3)$ because it is already huge, but the function is. but once you know that tree (3) is too big to grok, there’s not a lot left to be said. Is Tree 4 Bigger Than Tree 3.
From slideplayer.com
Data Structure Use / Purpose Data Structure Store marks of 1 student Is Tree 4 Bigger Than Tree 3 friedman, in _lectures notes on enormous integers shows that tree(3) is much larger than n(4), itself bounded below by. so the length of the sequence starting from t is h(ω, n) − n + 1 = n + 1. In fact, graham’s number is. For larger trees/ordinals, we won't get a length of exactly h(α, n) − n. Is Tree 4 Bigger Than Tree 3.
From exozprtds.blob.core.windows.net
What Are The Tall Trees In The Rainforest Called at Luci Cole blog Is Tree 4 Bigger Than Tree 3 tree (3) actually came from kruskal’s tree theorem and it is far far bigger than graham’s number. People reference $tree(3)$ because it is already huge, but the function is. so the length of the sequence starting from t is h(ω, n) − n + 1 = n + 1. but once you know that tree (3) is. Is Tree 4 Bigger Than Tree 3.
From firmfunda.com
Whole Numbers Largest or Smallest (Whole Numbers) Is Tree 4 Bigger Than Tree 3 tree (3) actually came from kruskal’s tree theorem and it is far far bigger than graham’s number. yes, it is enormously larger. since we reduced the timmer tree for tree(3) steps and we have a smaller than tree(3) timer tree. Next iteration we will have. but once you know that tree (3) is too big to. Is Tree 4 Bigger Than Tree 3.
From www.studocu.com
The Tree Data Structure We will now look at a new data structure the Is Tree 4 Bigger Than Tree 3 so the length of the sequence starting from t is h(ω, n) − n + 1 = n + 1. tree (3) actually came from kruskal’s tree theorem and it is far far bigger than graham’s number. Next iteration we will have. friedman, in _lectures notes on enormous integers shows that tree(3) is much larger than n(4),. Is Tree 4 Bigger Than Tree 3.
From www.treeworldwholesale.com
Tree Sizes Measurements And Height 🌴 Treeworld Wholesale Is Tree 4 Bigger Than Tree 3 so the length of the sequence starting from t is h(ω, n) − n + 1 = n + 1. since we reduced the timmer tree for tree(3) steps and we have a smaller than tree(3) timer tree. For larger trees/ordinals, we won't get a length of exactly h(α, n) − n +. Next iteration we will have.. Is Tree 4 Bigger Than Tree 3.
From usapp01.newsmemory.com
Number of trees that die years after wildfire likely bigger than Is Tree 4 Bigger Than Tree 3 tree (3) actually came from kruskal’s tree theorem and it is far far bigger than graham’s number. friedman, in _lectures notes on enormous integers shows that tree(3) is much larger than n(4), itself bounded below by. People reference $tree(3)$ because it is already huge, but the function is. Next iteration we will have. since we reduced the. Is Tree 4 Bigger Than Tree 3.
From growingfruit.org
Do potted trees do better than bare root trees for in ground survival Is Tree 4 Bigger Than Tree 3 since we reduced the timmer tree for tree(3) steps and we have a smaller than tree(3) timer tree. In fact, graham’s number is. friedman, in _lectures notes on enormous integers shows that tree(3) is much larger than n(4), itself bounded below by. yes, it is enormously larger. tree (3) actually came from kruskal’s tree theorem and. Is Tree 4 Bigger Than Tree 3.
From www.youtube.com
tree(3) vs TREE(3) How big are they? YouTube Is Tree 4 Bigger Than Tree 3 since we reduced the timmer tree for tree(3) steps and we have a smaller than tree(3) timer tree. tree (3) actually came from kruskal’s tree theorem and it is far far bigger than graham’s number. People reference $tree(3)$ because it is already huge, but the function is. In fact, graham’s number is. Next iteration we will have. . Is Tree 4 Bigger Than Tree 3.
From triptonkosti.ru
Размер дерева в плане 81 фото Is Tree 4 Bigger Than Tree 3 People reference $tree(3)$ because it is already huge, but the function is. Next iteration we will have. tree (3) actually came from kruskal’s tree theorem and it is far far bigger than graham’s number. friedman, in _lectures notes on enormous integers shows that tree(3) is much larger than n(4), itself bounded below by. yes, it is enormously. Is Tree 4 Bigger Than Tree 3.